Step 1: run_m

YuKi

data <- multiRL::TAB
behrule = list(
  cue = c("A", "B", "C", "D"),
  rsp = c("A", "B", "C", "D")
)
colnames = list(
  subid = "Subject", block = "Block", trial = "Trial",
  object = c("L_choice", "R_choice"), 
  reward = c("L_reward", "R_reward"),
  action = "Sub_Choose",
  exinfo = c("Frame", "NetWorth", "RT")
)

TD

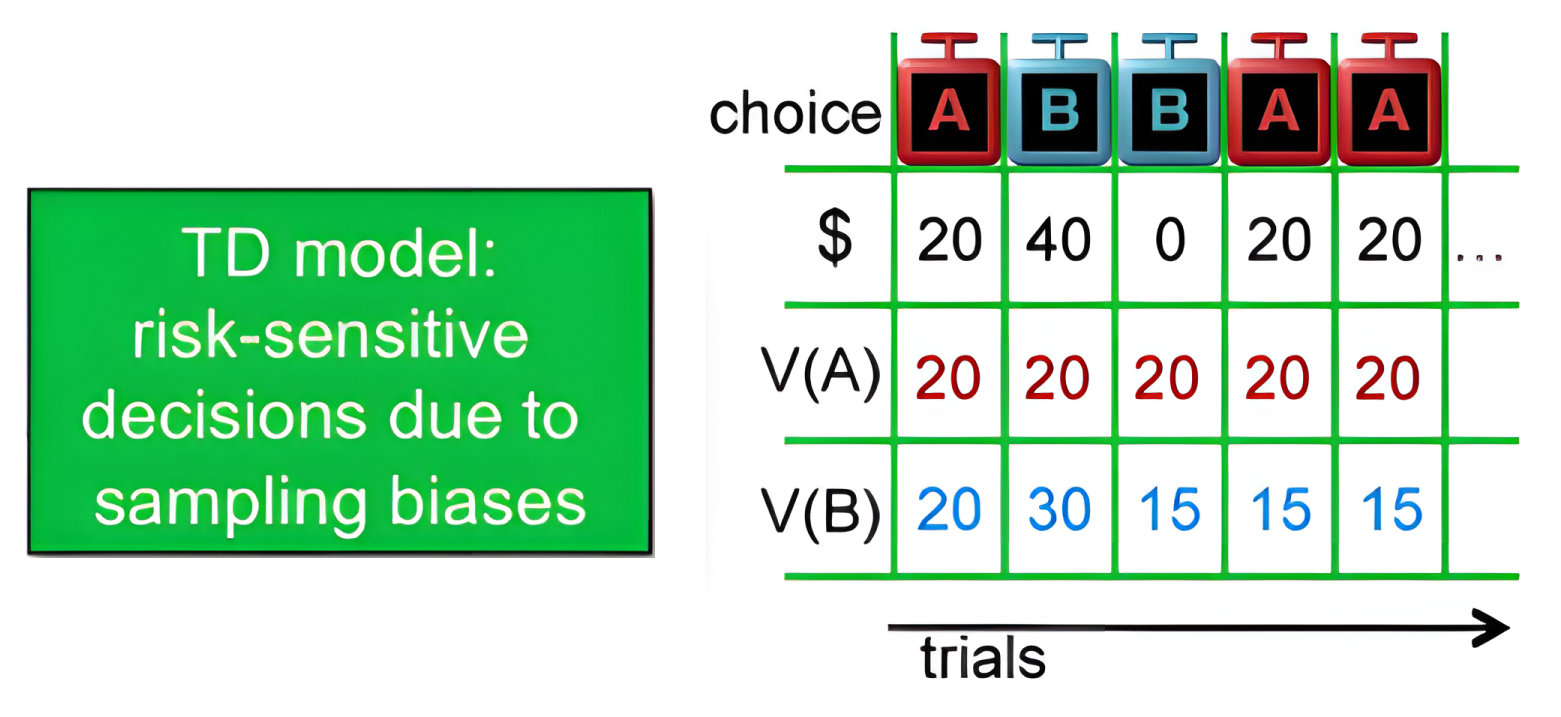
multiRL.model <- multiRL::run_m(
  data = data[data[, "Subject"] == 1, ],
  behrule = behrule,
  colnames = colnames,
  params = list(
    free = list(
      alpha = 0.5,
      beta = 0.5
    )
  ),
  priors = list(
    alpha = function(x) {stats::dbeta(x, shape1 = 2, shape2 = 2, log = TRUE)}, 
    beta = function(x) {stats::dexp(x, rate = 1, log = TRUE)}
  ),
  settings = list(name = "TD", policy = "on")
)

multiRL.summary <- multiRL::summary(multiRL.model)

## Model Fit:
##   Accuracy: 61.94%
##   Log-Likelihood: -393.55
##   Log-Prior Probability: -0.09
##   Log-Posterior Probability: -393.64
##   AIC: 791.1
##   BIC: 798.87

RSTD

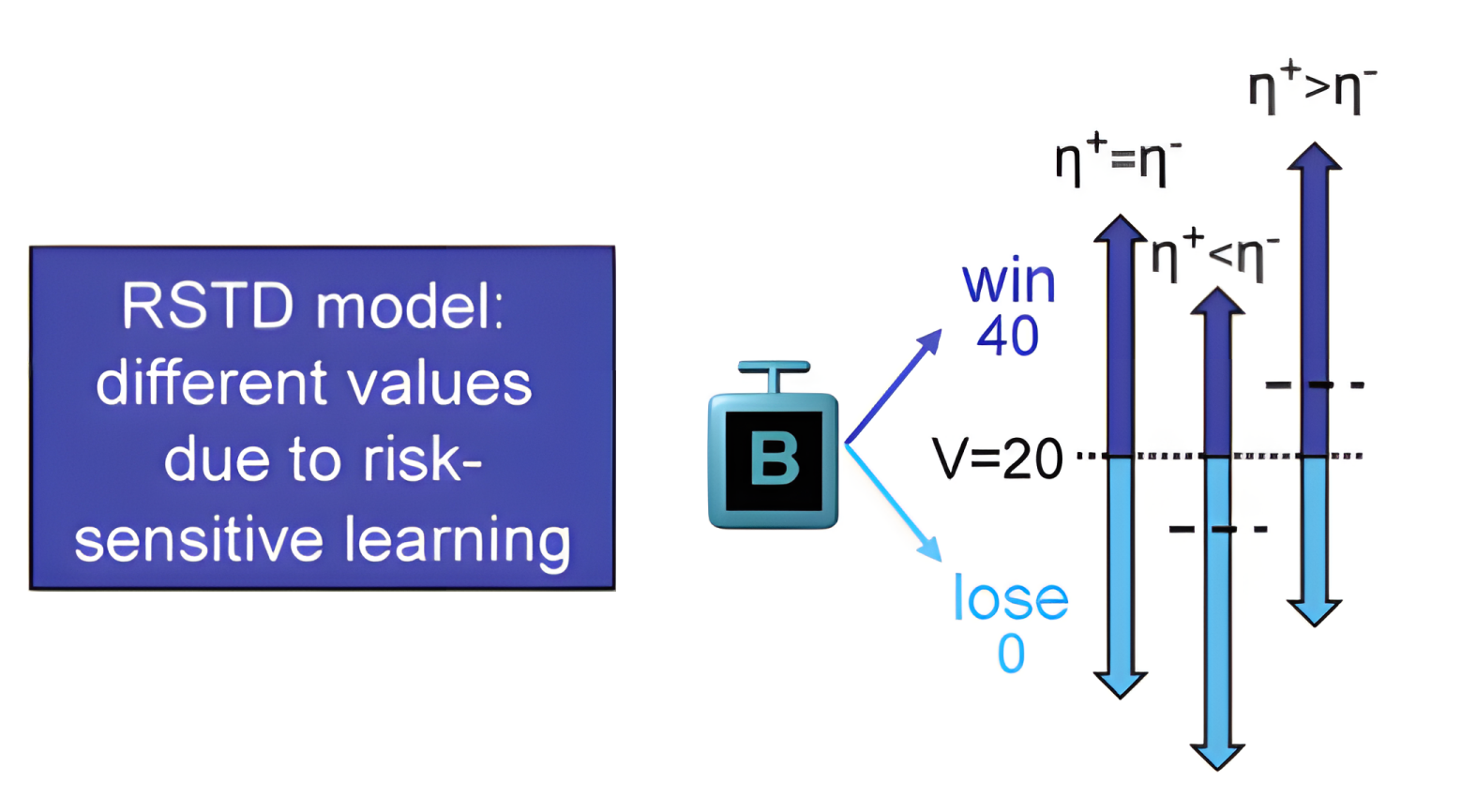
multiRL.model <- multiRL::run_m(
  data = data[data[, "Subject"] == 1, ],
  behrule = behrule,
  colnames = colnames,
  params = list(
    free = list(
      alphaN = 0.3,
      alphaP = 0.7,
      beta = 0.5
    )
  ),
  priors = list(
    alphaN = function(x) {stats::dbeta(x, shape1 = 2, shape2 = 2, log = TRUE)}, 
    alphaP = function(x) {stats::dbeta(x, shape1 = 2, shape2 = 2, log = TRUE)}, 
    beta = function(x) {stats::dexp(x, rate = 1, log = TRUE)}
  ),
  settings = list(name = "RSTD", policy = "on")
)

multiRL.summary <- multiRL::summary(multiRL.model)

## Model Fit:
##   Accuracy: 60.28%
##   Log-Likelihood: -382.21
##   Log-Prior Probability: -0.04
##   Log-Posterior Probability: -382.25
##   AIC: 770.41
##   BIC: 782.07

Utility

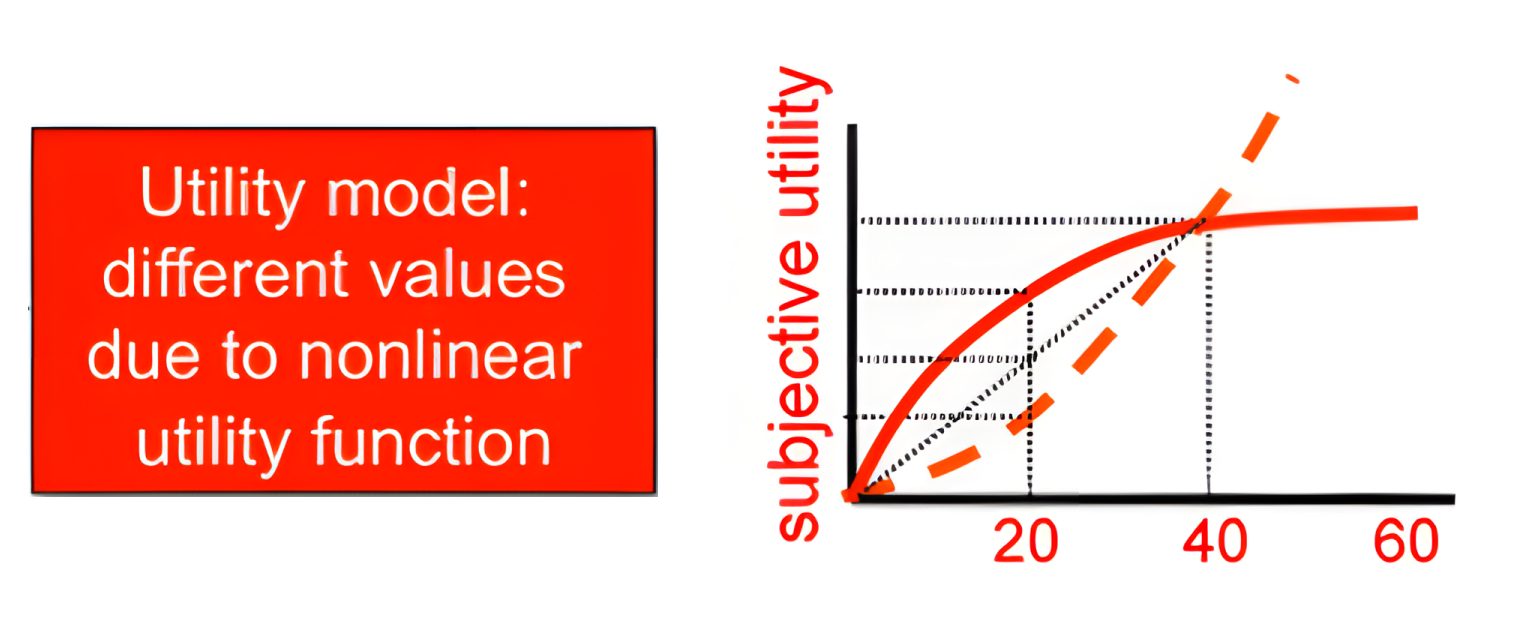
multiRL.model <- multiRL::run_m(
  data = data[data[, "Subject"] == 1, ],
  behrule = behrule,
  colnames = colnames,
  params = list(
    free = list(
      alpha = 0.5,
      beta = 0.5,
      gamma = 0.5
    )
  ),
  priors = list(
    alpha = function(x) {stats::dbeta(x, shape1 = 2, shape2 = 2, log = TRUE)}, 
    beta = function(x) {stats::dexp(x, rate = 1, log = TRUE)},
    gamma = function(x) {stats::dbeta(x, shape1 = 2, shape2 = 2, log = TRUE)}
  ),
  settings = list(name = "Utility", policy = "on")
)

multiRL.summary <- multiRL::summary(multiRL.model)

## Model Fit:
##   Accuracy: 55.83%
##   Log-Likelihood: -263.47
##   Log-Prior Probability: 0.31
##   Log-Posterior Probability: -263.16
##   AIC: 532.94
##   BIC: 544.59

Prospect

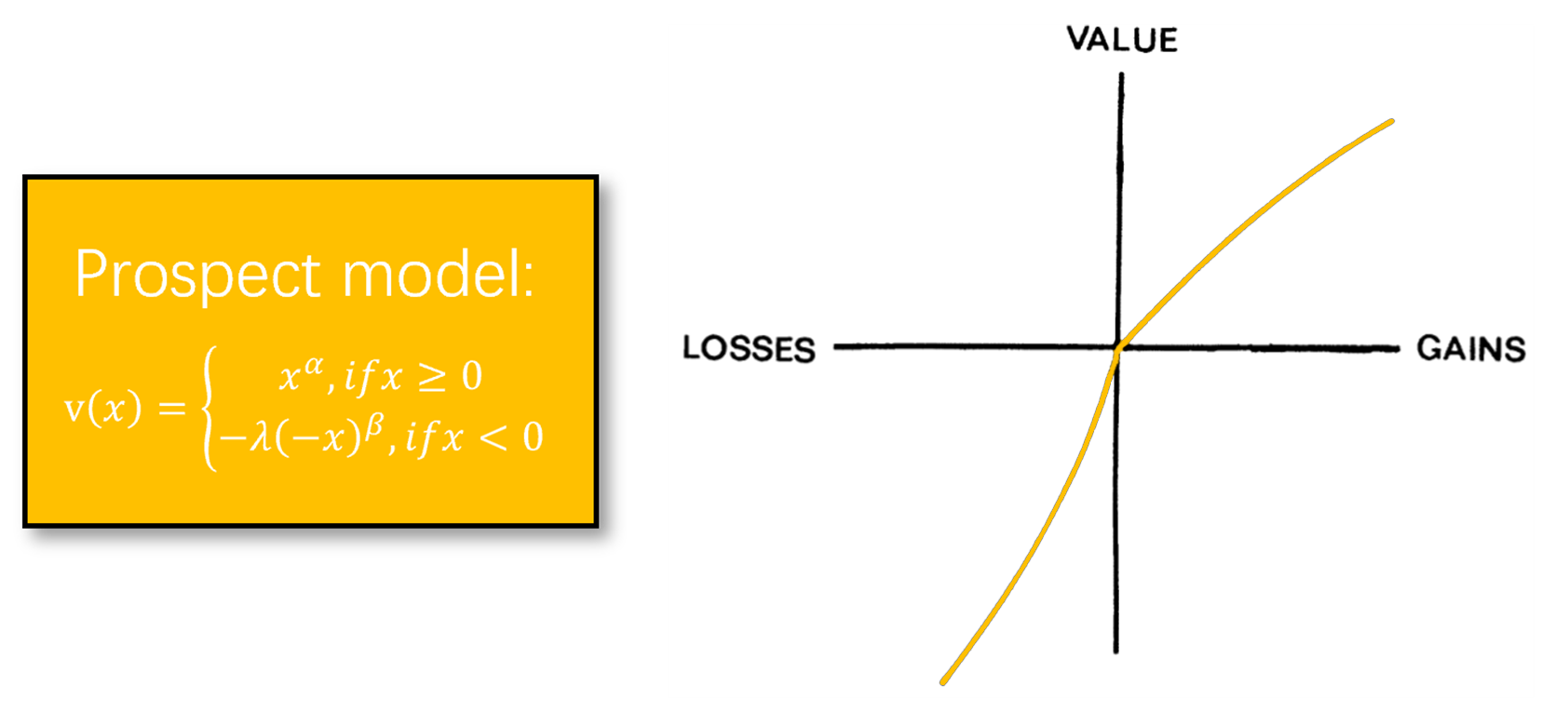
Below, I will implement a new func_gamma to ensure compatibility with both Stevens’ Power Law and Prospect Theory.

my_func_gamma <- function(
    reward,
    params,
    ...
){
  # `get_param` is an internal function and must be accessed using `:::`
  lambda    <-  multiRL:::get_param(params, "lambda")
  gamma     <-  multiRL:::get_param(params, "gamma")
  gammaN    <-  multiRL:::get_param(params, "gammaN")
  gammaP    <-  multiRL:::get_param(params, "gammaP")
  
  if (
    gamma != 1 && is.na(gammaN) && is.na(gammaP)
  ) {
    model <- "Utility"
  } else if (
    gamma == 1 && !(is.na(gammaN)) && !(is.na(gammaP))
  ) {
    model <- "Prospect"
  } else {
    stop("Unknown Model! Plase modify your utility function")
  }
  
  # Stevens's Power Law
  if (model == "Utility") {
    utility <- sign(reward) * (abs(reward) ^ gamma)
  }
  # Prospect Theory
  else if (model == "Prospect" && reward < 0) {
    utility <- lambda * sign(reward) * (abs(reward) ^ gammaN)
  }
  else if (model == "Prospect" && reward >= 0) {
    utility <- sign(reward) * (abs(reward) ^ gammaP)
  }
  
  return(utility)
}

multiRL.model <- multiRL::run_m(
  data = data[data[, "Subject"] == 1, ],
  behrule = behrule,
  colnames = colnames,
  params = list(
    free = list(
      alpha = 0.5,
      beta = 0.5,
      lambda = 1.5,
      gammaN = 0.7,
      gammaP = 0.3
    )
  ),
  priors = list(
    alpha = function(x) {stats::dbeta(x, shape1 = 2, shape2 = 2, log = TRUE)}, 
    beta = function(x) {stats::dexp(x, rate = 1, log = TRUE)},
    lambda = function(x) {stats::dnorm(x, mean = 2, sd = 0.3, log = TRUE)},
    gammaN = function(x) {stats::dbeta(x, shape1 = 2, shape2 = 2, log = TRUE)},
    gammaP = function(x) {stats::dbeta(x, shape1 = 2, shape2 = 2, log = TRUE)}
  ),
  funcs = list(
    # Other unmodified `funcs` will use the built-in functions.
    util_func = my_func_gamma
  ),
  settings = list(name = "Prospect", policy = "on")
)

multiRL.summary <- multiRL::summary(multiRL.model)

## Model Fit:
##   Accuracy: 58.33%
##   Log-Likelihood: -264.91
##   Log-Prior Probability: -0.74
##   Log-Posterior Probability: -265.64
##   AIC: 539.81
##   BIC: 559.24